这篇文章上次修改于 1123 天前,可能其部分内容已经发生变化,如有疑问可询问作者。
离散数学
笔者按:本文为笔者本科课程所作课堂笔记。学知所限,或有谬误,万望不吝斧正。
另,本文中10.1一节用到mermaid代码,本页不能正常渲染。
参考书:《离散数学及其应用》(第三版)
离散量
离散量:从一种程度开始,只要经过有限多种程度的逐次更替就能变化到另一种程度。
一、集合论
1.1 什么是集合
集合:一组对象
集合是由指定范围内的满足给定条件的所有对象聚集在一起构成,每一个对象成为这个集合的元素。
ZFC公理化集合论:外延公理 + 空集存在公理 + 无序对公理 + 并集公理 + 幂集公理 + 无穷公理 + 替换公理 + 正则公理 + 选择公理
用带或不带下标的大写英文字母表示集合:
用带或不带下标的小写英文字母表示元素:
若
是 中元素,记作 ,否则记作 。 表示方法
枚举法:
或 叙述法:
或 文氏图:图解方法。一般使用平面上的方形或圆形表示一个集合,用平面上的一个点表示集合的元素。(即韦恩图。)

基数
集合A中的元素个数称为集合的基数,记作
。 若一个集合的基数是有限的,则该集合称为有限集。
若一个集合的基数是无限的,则该集合称为无限集。
1.2 特殊集合和集合间关系
空集
不含任何元素的集合叫做空集,记作
。 空集可以符号化为
。 空集是绝对唯一的。
全集
针对一个具体范围,我们考虑的所有对象的集合叫做全集,记作
或 。 在文氏图中一般使用方形表示全集。
全集是相对唯一的。
集合的相等关系
元素的基本特性
- 集合中的元素是无序的。
- 集合中的元素是不同的。
外延性原理
两个集合
和 相等,当且仅当它们的元素完全相同,记为 ,否则 和 不相等,记为 。
子集和真子集
设
是任意两个集合。 - 如果
的每个元素都是 中的元素,则称 是 的子集,也称作 被 包含或 包含 ,记作 ,否则记作 。 - 如果
并且 ,则称 是 的真子集,也称作 被 真包含或 真包含 ,记作 ,否则记作 。
“
”关系的数学语言描述是: 。 
由子集定义可有
- 如果
证明集合相等
设
为任意两个集合,则 元集的子集 对于任意
元集合 ,它的 元 子集个数为 个,所以不同的子集个数为 。 幂集
设
为任意集合,把 的所有不同子集构成的集合叫做A的幂集,也叫集族或集合的集合,记作 ,即
1.3 集合的基本运算
并集
设
是两个集合,则集合 与 的并集定义为 交集
设
是两个集合,则集合 与 的交集定义为 补集
设
是全集,则集合 的补集定义为 差集
设
且 对称差集
设
且 或 且 并集和交集的扩展
设
或 或 或 设
且 且 且
1.4 集合的运算定律
集合运算的基本等式
设
集合相等的证明
如需证明集合A和B相等,则证明两个集合的相互包含关系,即
或者尝试反证:如果
,以及对称的情况,得出矛盾; 且 或者尝试改变A的写法,使其包含给定条件,然后代入条件,得出B。
1.5 可数集合与不可数集合
自然数集的定义
皮亚诺公理
- 每个自然数
- 两个自然数相等,当且仅当它们有相同的后继,即:
- 没有任何自然数的后继是0;
- (归纳公理)若
冯·诺依曼的自然数定义
- 若
从而,这个集合序列的基数就可以来定义自然数:
如何比较集合的大小
对于无限集合,通过判断两个无限集合之间是否存在一一对应关系来判断大小。
等势:设
若
,则 。反之不成立。
可数集合
凡与自然数集合
不可数集合
开区间
凡与开区间
第二章 计数问题
2.1 加法原理和乘法原理
乘法原理:如果一些工作需要
2.2 排列与组合
排列:从含
环形排列:含
2.3 容斥原理和鸽笼原理
容斥原理:设
第三章 命题逻辑
3.1 什么是命题
命题是推理的前提和结论。命题是推理的基本单位。
命题:具有确切真值的陈述句。该命题可以取一个“值”,称为真值。真值只有“真”和“假”两种,分别用“T”(或“1”)和“F”(或“0”)表示。
一切没有判断内容的句子,如命令句(祈使句)、感叹句、疑问句、二义性的陈述句等都不能作为命题。
我们无法判断真假的句子和句子本身是否有真假是两回事。例如:“今天是晴天。”
命题带变量如
,但却不对变量作任何限制,因为变量可以取甚至不是数,导致了二义性,因此不是命题。例如:“ ”不是命题。
原子命题(简单命题):不能再分解为更为简单命题的命题。
复合命题:可以分解为更为简单命题的命题。
约定:通常用大写的、带或不带下标的英文字母表示命题。
3.2 命题联结词
否定联结词
设
合取联结词
设
- 虽然……但是……
析取联结词
设
异或用单独的异或联结词
蕴涵联结词
设
- 如果
- 因为
- 只要
- 只有
- 除非
- 除非
善意推定:当前件
逆否命题:
等价联结词
设
3.3 命题符号化及其应用
命题联结词的真值表
命题联结词的优先级
否定 > 合取 > 析取 > 蕴涵 > 等价
同级的联结词从左到右;括号提升为最高优先级。
复合命题符号化
例:
:你陪伴我
:你代我叫车子
:我将出去 除非你陪伴我或代我叫车子,否则我将不出去。
或
命题联结词与开关电路
串联:
并联:
断开:
命题联结词与逻辑电路
与门:
或门:
非门:
命题联结词与网页检索
命题联结词与位运算
- 按位与
- 按位或
- 按位取反
3.4 命题公式和真值表
命题变元
一个特定的命题是一个常值命题,它要么具有值
一个任意的没有赋予具体内容的原子命题是一个变量命题,称为命题变量或命题变元。该命题变量无具体的真值,它的变域是集合
一个复合命题的原子命题是命题变元时,该复合命题是命题公式。
命题公式
命题演算的合式公式,又称命题公式,简称公式。
生成规则:
命题变元本身是一个公式;
如
如
仅由有限步使用1. 2. 3. 后所得到的包含命题变元、联结词和括号的符号串才是命题公式。
如果公式
原子命题变元是最简单的合式公式,称为原子合式公式,简称原子公式。
命题公式没有真值,只有对其命题变元进行真值指派后,命题公式的真值才能确定。
整个公式的最外层括号可以省略;公式中不影响运算次序的括号也可以省略。
命题公式常用二元树的方式来表达。
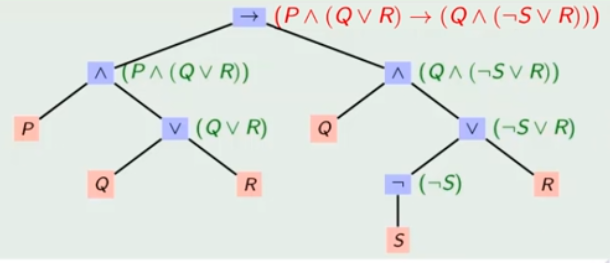
公式的解释
设
如果公式
如果公式
真值表
一般来说,若有
由公式G在其所有可能的解释下所取真值得到的表,称为真值表。
3.5 命题公式分类和等价
命题公式分类
公式
公式
公式
若
等价
设
对于任意两个公式G和H,
可判定性:能否给出一个可行方法,完成对任意公式的判定类问题。命题公式是可判定的。
3.6 命题等价公式及应用
命题等价公式
设
判断公式类型
开关电路化简
逻辑电路化简
3.7 范式
基本术语
文字:命题变元或命题变元的否定。例如:
简单析取式(子句):有限个文字的析取。例如:
简单合取式(短语):有限个文字的合取。
析取范式:有限个短语(简单合取式)的析取式。例如:
合取范式:有限个子句(简单析取式)的合取式。
是一个文字、短语、子句、析取范式、合取范式;
是子句、合取范式、析取范式;
是子句、合取范式,但不是析取范式。
不是析取或合取范式,但去掉括号则是。 以
框起的部分算作一个整体,不可拆分。
范式关注的是命题公式的当前书写形式。
单个的文字是子句、短语、析取范式、合取范式。
析取、合取范式只含有联结词集
范式存在定理
定理 任意公式都存在与其等价的析取范式和合取范式。
命题公式的范式表达并不唯一。
范式与真值
命题公式的析取范式可以指出公式何时为真;
命题公式的合取范式可以指出公式何时为假。
3.8 主范式
极小项和极大项
在含有
极小项:短语。非
极大项:子句。非
性质
主析取范式和主合取范式
主析取范式:在给定的析取范式中,若每一个短语都是极小项,且按照编码从小到大的顺序排列,则称该范式为主析取范式。
主合取范式:在给定的析取范式中,若每一个子句都是极大项,且按照编码从小到大的顺序排列,则称该范式为主合取范式。
如果一个主析取范式不包含任何极小项,则称该主析取范式为“空”;
如果一个主合取范式不包含任何极大项,则称该主合取范式为“空”;
定理 任何一个公式都有与之等价的主析取范式和主合取范式。
主范式求解定理
求出该公式所对应的析取范式和合取范式;
消去重复出现的命题变元,矛盾式或重言式;
若析取(合取)范式的某一个短语(子句)中缺少命题变元
重复至所有短语或子句都是标准的极小项或极大项为止。
利用幂等律将重复的极小项和极大项合并,并利用交换律进行顺序调整,由此可转换成标准的主析取范式和主合取范式。
真值表技术
考虑任意公式
若某一种解释使得
极大项反之。
主范式的应用
如果主析取范式包含所有的极小项,则该公式为永真公式;
如果主合取范式包含所有的极大项,则该公式为永假公式;
若两个公式具有相同的主析取范式或主合取范式,则两公式等价。
3.9 基本推理形式和蕴含公式
推理形式
推理:从一组前提合乎逻辑地推出结论的思维过程。
设
称
的优先级为 。等价于 。
推理的判定定理
定理 公式
推理定律——基本蕴含关系
设
3.10 自然演绎法推理
推理规则
前提引用规则(规则
逻辑结果引用规则(规则
附加前提规则(规则
自然演绎法
从前提集合
直接证明法
已知结论和条件,尝试倒推,“缺谁证谁”,即可写出证明。
例:前提
,结论 。证明 。 附 加 前 提
间接证明法
- 反证法
- 归谬法
要证明:
根据判定定理:
即,
因此:
总可以不使用反证法而用规则
代替。 也即,反证法是规则
的一种变型。 反证法:
, 根据规则
: , 即,
。 即:
。
3.11 联结词的完备集〔扩展内容〕
联结词的扩充
| 联结词 | 记号 | 复合命题 | 读法 | 记法 | 真值 |
|---|---|---|---|---|---|
| 异或 | |||||
| 蕴涵否定 | 只有 |
||||
| 与非 | 只有 |
||||
| 或非 | 只有 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
联结词的完备集
设
若
第四章 谓词逻辑
4.1 谓词的引入
谓词逻辑(一阶逻辑):为了研究简单命题句子内部的逻辑关系,利用个体词、谓词和量词来描述简单命题,以对简单命题进行分解,并研究个体与总体的内在联系和数量关系。
个体词和谓词
命题是具有真假意义的陈述句。从语法上分析,一个陈述句由主语和谓语两部分组成。
个体词:在原子命题中,可以独立存在的客体(句子中的主语、宾语等)。
谓词:用以刻画客体的性质或客体之间的关系。
个体词
- 个体常量:表示具体或特定的个体词。一般用带或不带下标的小写英文字母
- 个体变量:表示抽象的或泛指的个体词。一般用带或不带下标的小写英文字母
- 个体域(论域):个体词的取值范围。常用
- 全总个体域:宇宙间的所有个体域聚集在一起所构成的个体域。若无特别说明,均使用全总个体域。
谓词
设
- 谓词常量:表示具体性质或关系的谓词。
- 谓词变量:表示抽象的或泛指的性质或关系的谓词。
谓词均使用大写字母
谓词中个体词的顺序不能随意变更。例,
一元谓词用以描述某一个个体的某种特性,而
谓词
一般将没有任何个体变量的谓词称为0元谓词,例如
复合命题的谓词符号化
例:如果张三是一个三好学生,那么他的学习一定很好。
设
: 是一个三好学生, : 学习成绩好, :张三 则该命题符号化为:
4.2 量词的引入
量词
- 全称量词
- 存在量词
其中的
更准确的表达
例:所有的老虎都要吃人。
不准确的符号化表达
: 要吃人。
老 虎 更准确的符号化表达
: 是老虎, : 要吃人。
例:有一些人登上过月球。
不准确的符号化表达
: 登上过月球。
人 更准确的符号化表达
: 是人, : 登上过月球。
谓词逻辑符号化的两条规则
统一个体域为全总个体域,而对于每一个句子中个体变量的变化范围用一元特性谓词刻画之。这种特性谓词在加入到命题函数中时必须遵循如下规则:
- 对于全称量词
- 对于存在量词
量词相关的真值确定
当个体域
4.3 谓词符号化举例
谓词符号化
例:没有人登上过木星。
令
: 是人, : 登上过木星。
或
例:在美国留学的学生未必都是亚洲人。
令
: 是亚洲人, : 是在美国留学的学生。
或
二元谓词
例:天下乌鸦一般黑。
令
: 是乌鸦, : 与 一般黑。
或
假定个体域
例:每个实数都存在比它大的另外的实数。
令
: 是实数, : 小于 。
$ 若假定个体域为所有实数,则命题符号化为
多句话
例:所有狮子都是凶猛的;有些狮子不喝咖啡;有些凶猛的动物不喝咖啡。
令
: 是狮子; : 是凶猛的; : 喝咖啡。 假定所有动物的集合为个体域。
例:所有的蜂鸟都五彩斑斓;没有大鸟以蜜为生;不以蜜为生的鸟都色彩单调;蜂鸟都是小鸟。
令
: 是蜂鸟; : 是大鸟; : 是以蜜为生的鸟; : 五彩斑斓。 假定所有鸟的集合为个体域。
常量的使用
例:只要是需要室外活动的课,郝亮都喜欢;所有的公共体育课都的需要室外活动的课;篮球是一门公共体育课;郝亮喜欢篮球这门课。
令
: 的需要室外活动的课; : 喜欢 ; : 是一门公共体育课; :郝亮; :篮球。
4.4 谓词公式
符号
- 常量符号:指所属个体域
- 变量符号:指所属个体域
- 函数符号:
- 谓词符号:
项
- 任意的常量符号或任意的变量符号是项;
- 若
- 仅由有限次使用以上两个规则产生的符号串才是项。
合式公式
若
合式公式(公式)
- 原子公式是合式公式;
- 若
- 由有限次使用以上三个规则产生的表达式才是合式公式。
公式的最外层括号可省略。
量词后面的括号省略方式为:一个量词的辖域中仅出现一个原子公式,则此辖域的外层括号可省略,否则不能省略。
一个个体词只能受一个量词的约束,否则就是没有意义的。
4.5 自由变元和约束变元
自由变元和约束变元
给定一个合式公式
辖域
- 若量词后有括号,则括号内的子公式就是该量词的辖域;
- 若量词后有括号,则与量词邻接的子公式就是该量词的辖域。
变元改名规则
- 约束变元的改名规则
- 将量词中的变元以及该量词辖域中此变量之所有约束出现都用新的个体变元替换;
- 新的变元一定要有别于改名辖域中的所有其他变量。
- 自由变元的代入规则
- 将公式中出现该自由变元的每一处都用新的个体变元替换;
- 新的变元不允许在原公式中以任何约束形式出现。也可用个体常量代入。
闭式
设
显然,闭式是一个命题。
4.6 谓词公式的解释和分类
公式的解释
谓词逻辑中公式
- 非空的个体域集合
规定:公式中无自由变元,或将自由变元看成是常量符号。
公式的分类
有效公式:公式
矛盾公式:公式
可满足公式:至少有一种解释使得公式
公式的判定问题
谓词逻辑是不可判定的;
只含有一元谓词变项的公式是可判定的;
如下形式的公式:
个体域有穷时的谓词公式是可判定的。
4.7 谓词公式的等价关系
等价
如果公式
设
定理 永真公式的任意一个代入实例必为有效公式。
谓词演算中的基本等价公式
命题公式中的基本等价公式
假设
下面四条公式
~ 中的 不能有 。
对于多个量词的公式,设
4.8 前束范式〔扩展内容〕
前束范式
称公式
其标准形式如下:
前束范式的求解步骤
- 消去公式中的联结词
- 反复运用量词转换律、德摩根律和双重否定律,直到将所有的
- 使用谓词的等价公式将所有量词提到公式的最前端并保证其辖域直到公式的末端。
4.9 推理形式和推理规则
推理形式
设
定理 设
推理规律
命题演算中的基本蕴涵公式
假设
对于多个量词的公式,设
全称特指规则US
或:
存在特指规则ES
当
全称推广规则UG
存在推广规则EG
或:
4.10 综合推理方法
谓词的演绎推理
假定推导过程都是在相同的个体域内进行的(通常是全总个体域)。
综合推理方法
- 推导过程中可以引用命题演算中的规则P和规则T;
- 如果结论是以条件形式或析取形式给出,则可使用规则CP;
- 若需消去量词,可以引用规则US和规则ES;
- 当所求结论需定量时,可引用规则UG和规则EG引入量词;
- 证明时可采用如命题演算中的直接证明方法和间接证明方法;
- 在推导过程中,对消去量词的公式或公式中不含量词的子公式,可以引用命题演算中的基本等价公式和基本蕴涵公式;
- 在推导过程中,对含有量词的公式可以引用谓词中的基本等价公式和基本蕴涵公式。
例:证明
难点:
- 在推导过程中,如既要使用规则US又要使用规则ES消去量词,而且选用的个体是同一个符号,则必须先使用规则ES,再使用规则US。然后再使用命题演算中的推理规则,最后使用规则UG或规则EG引入量词,得到所求结论。
- 如一个变量是用规则ES消去量词,对该变量在添加量词时,则只能使用规则EG;如使用规则US消去量词,对该变量在添加量词时,则可使用规则EG和规则UG。
- 在用规则US和规则ES消去量词时,此量词必须位于整个公式的最前端,且辖域为其后的整个公式。
- 在添加量词
例:反证法
证明
附 加 前 提
如有两个含有存在量词的公式,当用规则ES消去量词时,不能选用同样的一个常量符号来取代两个公式中的变元,而应用不同的常量符号来取代它们。
第五章 证明技术
5.2 证明定理的方法
在定理证明中,如果将证明中的已知看成是命题逻辑中的前提,将证明的结果看成是命题逻辑中的结论,则大多数定理都是一个蕴涵关系。
要证明逻辑关系
基本证明技术
直接证明
间接证明
因为
几种典型的证明技术
空证明:
平凡证明:
归谬法证明:反证法
分情形证明:
为了证明形如
等价性证明:
为了证明一个定理是双条件的,即形如
存在性证明
构造性证明
惟一性证明
5.3 数学归纳法
数学归纳法原理
假设要证明的命题能写成形式:
即:希望证明对所有的整数
假设
- 归纳基础:验证
- 归纳假设:假设对于
- 归纳结论:证明
结论 对所有的整数
强形式数学归纳法原理
假设
- 归纳基础:验证
- 归纳假设:假设对于
- 归纳结论:证明
结论 对所有的整数
第六章 二元关系
6.1 序偶和笛卡尔积
有序组的定义
由两个元素按照一定的次序组成的二元组称为序偶,记作
两个序偶
笛卡儿积
设
性质
- 设
- 设
- 当集合
- 笛卡儿积对并运算和交运算满足分配律。
推广
由
设
性质
- 两个
- 当集合
6.2 关系的定义
二元关系
设
其中,
数学符号
- 若序偶
- 若序偶
几种重要关系
- 当
- 当
- 当
有限集合的二元关系数量
当集合
定义域和值域
设
称
二元关系概念的推广
设
在
6.3 关系的表示
关系的集合表示
关系是一种特殊的集合,因此集合的两种基本表示法(枚举法和叙述法),可以用到关系的表示中。
关系的图形表示
设
- 集合中的元素
- 如果
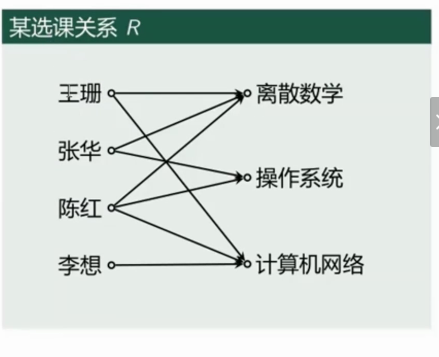
- 如果
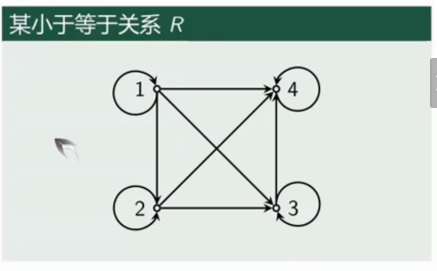
关系的矩阵表示
设
例:上面选课关系
的邻接矩阵
布尔矩阵的并和交运算
如果
如果
布尔矩阵的积运算
如果
6.4 关系的运算
关系的并交差补运算
关系是一种特殊的集合,因此集合的所有基本运算(并、交、差、补),都可以应用到关系中,并且同样满足集合的所有运算定律。
设
关系的复合运算
设
用三种关系表示法进行复合运算
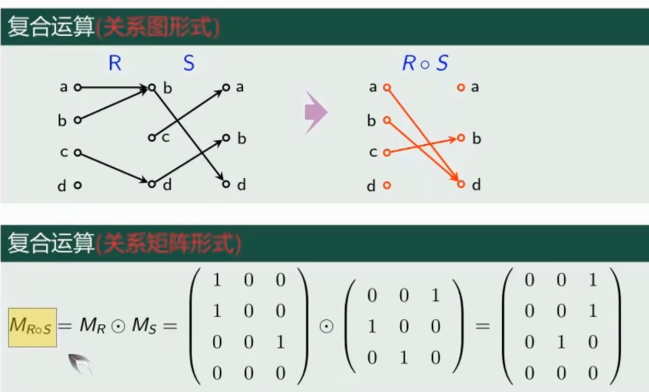
- 集合表示法:寻找所有满足
- 关系图表示法:将关系
- 关系矩阵表示法:将关系
关系的逆运算
设
用三种关系表示法求逆
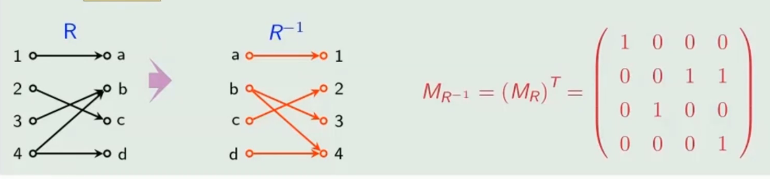
- 集合表示法
- 关系图表示法:将
- 关系矩阵表示法:将关系
6.5 关系的运算定律
结合律与同一律
设
目标:证明两个关系
也即证明两个集合
分配律
设
逆运算性质定律
设
6.6 关系的幂运算
关系的幂运算
设
幂运算的性质
的基数并非随着 的增加而增加,而是呈递减趋势。 当
时,则 。
定理 设
6.7 关系的性质(一)
自反性与反自反性
设
- 如果对任意的
- 如果对任意的
存在既不是自反的也不是反自反的关系;
关系
关系
对称性与反对称性
设
- 如果对任意的
- 如果对任意的
存在既不是对称的也不是反对称的关系,也存在既是对称又是反对称的关系;
既是对称的,又是反对称的。 因为,反对称要求在
时没有对称关系;在 时,没有要求。
关系
关系
传递性
设
一个特殊例子:
是传递的。
关系
关系
6.8 关系的性质(二)
关系性质的判定定理
设
关系性质判定
| 自反性 | 反自反性 | 对称性 | 反对称性 | 传递性 | |
|---|---|---|---|---|---|
| 定义 | |||||
| 关系运算 | |||||
| 关系图 | 每个结点都有环 | 每个结点都无环 | 任两结点间,要么没有边,要么有方向相反的两条边 | 任两结点间,至多有一条边 | 如果从 |
| 关系矩阵 | 主对角线上全为1 | 主对角线上全为0 | 对称矩阵 |
一个关系可能满足多种性质,如:
- 非空集合
上的全关系 :自反,对称,传递 - 非空集合
上的空关系 :反自反,对称,反对称,传递 - 非空集合
上的恒等关系 :自反,对称,反对称,传递 - 实数集
上的等于关系 :自反,对称,反对称,传递 - 幂集上的真包含关系
:反自反,反对称,传递
关系性质的保守性
设
- 若
- 若
- 若
- 若
- 若
| 自反 | √ | √ | √ | √ | |
| 反自反 | √ | √ | √ | √ | |
| 对称 | √ | √ | √ | √ | |
| 反对称 | √ | √ | √ | ||
| 传递 | √ | √ |
第七章 特殊关系
7.1 等价关系
等价关系定义
设
等价关系的关系图类似下图:
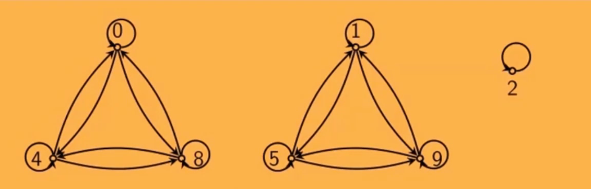
即,等价关系是多个“小集合”的全关系组合而成。
要证明一个等价关系,就要证明该关系是自反的、对称的、传递的。
等价类
设
定理 设
- 对任意
- 对任意
商集
设
计算商集
- 任选
- 如果
- 如果
- 以此类推,直到
7.2 集合的划分
定义
给定一个非空集合
则集合
等价划分
定理 设
等价关系导出
定理 给定集合
7.3 偏序关系定义
定义
设
不是经典的“小于等于”。
当
可比与覆盖
设
例:对于整除关系,有4和6覆盖2:
2可以整除4,2可以整除6,但4不可以整除6。即,对于6,
。
7.4 哈斯图及特殊元素
哈斯图
设
- 取消每个结点的自环;
- 取消所有由于传递性出现的边。即若
- 重新排列每条边,使得边的箭头方向全部向上,然后去掉这些箭头。
以上步骤可以得到一个包含足够偏序信息的图,这个图称为偏序关系
设
, 是 上的整除关系 。 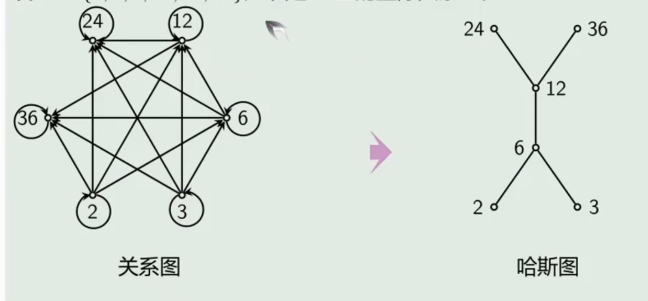
特殊元素
最大元和最小元
设
- 对任意
- 对任意
如果不可比,则不存在最大元、最小元。
极大元和极小元
设
- 对任意
- 对任意
如果不可比,则都是极大元、极小元。
总结
上界和上确界
设
- 对任意
- 若元素
下界和下确界
设
- 对任意
- 若元素
总结
子集
子集
子集
若子集
因为上(下)界中的元素不一定都可比。
总结
- 若
- 若
- 若
- 若
- 集合
- 集合
7.5 其它次序关系
拟序关系
设
定理 设
若
是集合 上的偏序关系,则 是 上的拟序关系; 若
是集合 上的拟序关系,则 是 上的偏序关系。
全序关系
设
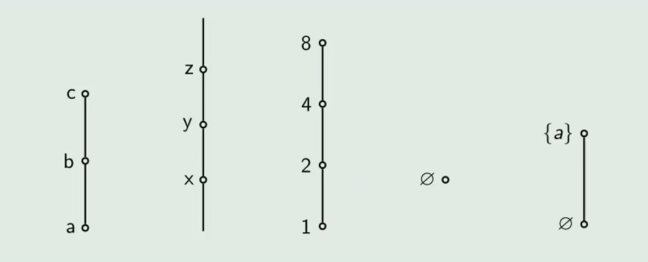
全序关系的哈斯图将集合中的元素排成一条线,像一条链子,这充分体现了全序集可以称作线序集或链的原因。
良序关系
设
良序关系一定是全序关系,而有限全序集一定是良序集。
总结
偏序关系、全序关系和良序关系之间的关系如下图:

第八章 函数
8.1 函数基本定义
定义
设
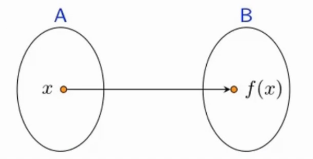
当
如果关系
- 存在元素
- 存在元素
所有从
函数的数量
设函数
关系与函数的差别
当
- 关系和函数的数量不同:从
- 关系和函数的基数不同:每一个关系的基数可以从零一直到
- 关系和函数的第一元素存在差别:关系的第一个元素可以相同,函数的第一元素一定是互不相同的。
8.2 函数的类型
函数的类型
设
- 对任意
- 如果
- 如果
必要条件
若
函数类型的数学化描述
典型(自然)映射
设
函数类型证明
根据数学化描述证明。
证明单射可以考虑反证。例如:对任意
证明满射可以考虑包含关系。例如:有
8.3 函数的运算
函数的复合
设
函数
对任意
复合运算的保守性
设
- 设
- 设
- 设
如
是从 到 的满射,则 是从 到 的满射; 如
是从 到 的单射,则 是从 到 的单射; 如
是从 到 的双射,则 是从 到 的单射, 是从 到 的满射。
函数的逆
设
函数
第九章 图论基础
9.1 图的引入
不同类型的图
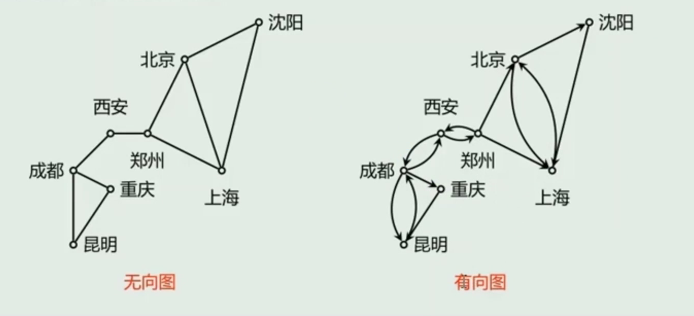
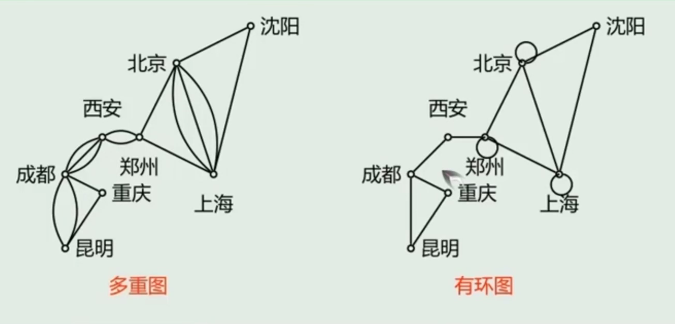
无序对和无序积
设
与序偶不同,对
。
图的定义
一个图是一个序偶
与边对应的结点对既可以是无序的,也可以是有序的。
若边
若边
9.2 图的表示
集合表示和图形表示
图的集合表示:对于一个图
图的图形表示:用小圆圈表示
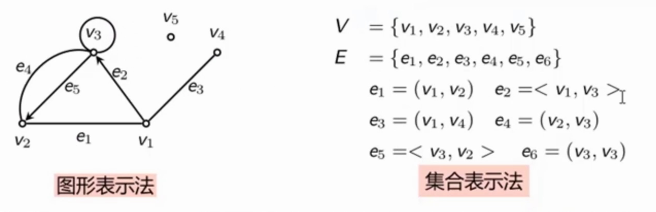
邻接矩阵
设图
邻接点与邻接边
在图
一些简单的特殊图
- 零图:仅由孤立结点组成的图;
- 平凡图:仅含一个结点的零图;
环的存在与否不会导致图论定理的重大变化,很多场合下都会被忽略;
零图没有任何边,邻接矩阵为全0;
9.3 图的分类
按边有无方向分类
每条边都是无向边的图称为无向图;
每条边都是有向边的图称为有向图;
有些边是无向边,而另一些边是有向边的图称为混合图。
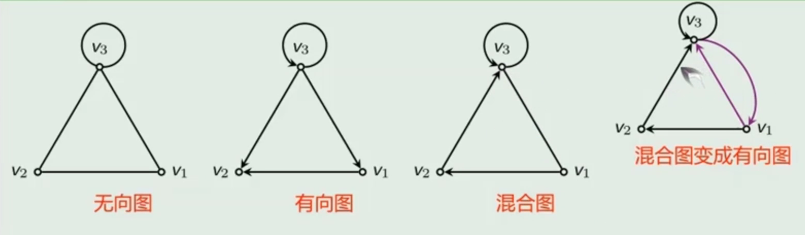
按有无平行边分类
在有向图中,两结点间(包括结点自身间)若有同始点和同终点的几条边,则这几条边称为平行边;
在无向图中,两结点间(包括结点自身间)若有几条边,则这几条边称为平行边。
两结点
含有平行边的图称为多重图;
非多重图称为线图;
无环的线图称为简单图。
按有无权值分类
赋权图
相应的,边或结点均无权值的图称为无权图。
9.4 子图和补图
各类子图
设有图
若
若
若
生成子图:相对于原图,全部的结点都在。
设
导出子图:相对于原图,只要结点还在,其对应的全部的边都在。
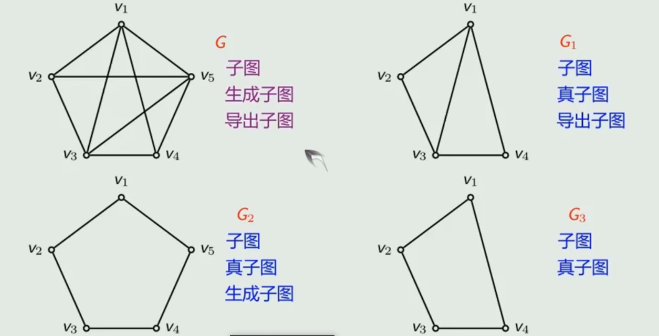
完全图
设
设
- 完全图的邻接矩阵除主对角线上的元素为0外,其余元素均为1;
- 无向完全图
- 有向完全图
补图
设
- 补图
- 补图
- 图
邻接矩阵求补图的方法
若设简单图
9.5 握手定理
结点的度数
图
有向图
图
有向图
设图
- 若
- 若
握手定理
定理 图中结点度数的总和等于边数的二倍,即设图
常称度数为奇数的结点为奇度数结点,度数为偶数的结点为偶度数结点。
定理 有向图中各结点的出度之和等于各结点的入度之和,等于边数,即设有向图
设
9.6 图的同构
引言
即,两个图本质上是同一个图。
定义
设两个图
形象地说,若图的结点可以任意挪动位置,而边是完全弹性的,只要在不拉断的条件下,一个图可以变形为另一个图,那么这两个图是同构的。
必要条件
- 结点数目相同
- 边数相同
- 度数相同的结点数相同
可以通过同构的必要条件不满足说明两个图不同构。
但不能作为充分条件使用。即使满足这三个条件,也不一定是同构。
9.7 通路和回路
通路和回路
给定图
- 若
- 若通路中的所有边互不相同,则称此通路为简单通路,否则称为复杂通路;若回路中的所有边互不相同,则称此回路为简单回路,否则称为复杂回路。
- 若通路中的所有结点互不相同,所有边也互不相同,则称此通路为基本通路或者初级通路;若回路中除
回路是通路的特殊情况。
在不会引起误解的情况下,一条通路可以用边的序列
在简单图中,一条通路也可以用结点的序列
通路数量
定理 设
就是对矩阵 求 次幂。
推论 设矩阵
9.8 可达性和最短通路
可达性
在图
规定 任何结点到自己都是可达的。
定理 在一个具有
推论 在一个具有
定理 在一个具有
推论 在一个具有
定理 设
设
定理 设
最短通路
如果
定理 设
9.9 无向图的连通性
无向图的连通性
若无向图
- 无向完全图
- 多于一个结点的零图都是非连通图;
- 非平凡无向线图
定理 无向图
无向图
点割集与边割集
图的删除操作
对于一个无向图
点割集
设无向图
边割集
设无向图
连通度
设无向连通图
- 称
为 的 点 割 集 或 为 平 凡 图 - 称
为 的 边 割 集
若
若
若
若
9.10 有向图的连通性
有向图的连通性
由于有向图中边都有方向性,因此有向图结点之间的可达关系仅仅具有自反性和传递性,而不具有对称性。因此,有向图中的可达关系不是等价关系。
设
- 略去
- 若
- 若
显然,强连通图必是单向连通图;单向连通图必是连通图。但反之均不成立。
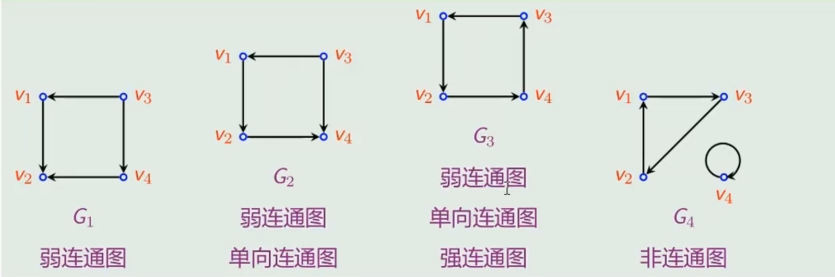
判定
有向图
有向图
邻接矩阵判定
由邻接矩阵
- 有向线图
- 有向线图
- 有向线图
连通分支
在有向图
- 对任意
那么称
弱连通分支也就是忽略边的方向所对应的无向图的连通分支;
注意把握强(单向、弱)连通分支的极大性特点,即,任意增加一个结点或一条边就不是强(单向、弱)连通的了。
判定
在有向图
在有向图
- 弱连通分支:图的不互连部分
- 强连通分支:出度为0或入度为0的结点,极大回路,……
- 单向连通分支:极大通路
9.11 最短通路问题
设
- 该图中一条通路上所有边的权值之和,称为这条通路的长度;
- 两个结点间长度最短的通路,称为这两个结点间的最短通路。
单源点的最短通路——Dijkstra算法
基本思想
- 将结点集合
- 所谓结点
- 首先将
初始化:将源结点
找最小:寻找具有最小值的
修改:修改与
重复2-3,直到所有结点都改为
任意两点间的最短通路——Floyd算法
基本思想
- 设
- 若已知
两种算法的比较
- Dijkstra算法求指定结点到其它结点间的最短通路,Floyd算法求出任意两点间的最短通路;
- 在求解多源最短路径问题上,二者的时间复杂度相当,都是
- 二者均能处理无向赋权图和有向赋权图;
- Dijkstra算法不能求解有负权边的图,而Floyd算法可以求解带负权边的图。
第十章 树
10.1 认识树
树的模型
graph TD
1 --> 2 --> 4 --> 7
1 --> 3 --> 5
3 --> 6 --> 9
4 --> 8树的应用
- 二元搜索树
- 决策树
- 前缀码(配合哈夫曼算法)
10.2 无向树
定义
连通而不含回路的无向图称为无向树,简称树,常用
树中度数为1的结点称为叶;度数大于1的结点称为分支点或内部结点。
每个连通分支都是树的无向图称为森林。
平凡图称为平凡树。
容易看出,树中没有环和平行边,因此一定是简单图,并且在任何非平凡树中,都无度数为0的结点。
一棵树也可以叫做森林。
树的性质(等价定义)
定理 设无向图
特点
在结点给定的无向图中,
- 树是边数最多的无回路图;
- 树是边数最少的连通图。
由此可知,在无向图
- 若
- 若
性质应用
定理 任意非平凡树
10.3 生成树
定义
给定图
- 若
生成树存在的条件
定理 一个图
算法
求连通图
破圈法
循环找到图中的回路并删除回路中的一条边,直到删除的边的总数为
避圈法
循环选取
生成树的广度优先搜索算法
连通图
- 任选
- 如果
- 依次对
10.4 最小生成树
定义
设
一个无向图的生成树不是唯一的,同样地,一个赋权图的最小生成树也不一定是唯一的。
Kruskal算法
其要点是,在与已选取的边不构成回路的边中选取最小者。
- 在
- 当
- 在
- 置
Prim算法
其要点是,从任意结点开始,每次增加一条最小权边构成一棵新树。
- 在
- 在
- 重复步骤⒉,直到
10.5 根树
定义
一个有向图,若略去所有有向边的方向所得到的无向图是一棵树,则这个有向图称为有向树。
一棵非平凡的有向树,如果恰有一个结点的入度为0,其余所有结点的入度均为1,则称之为根树或外向树,出度为0的结点称为叶;入度为1,出度大于0 的结点称为内点;又将内点和根统称为分支点。
在根树中,从根到任一结点
习惯上使用倒置法来画根树,即把根画在最上方,叶画在下方,有向边的方向均指向下方,这样就可以省去全部的箭头,不会发生误解。
家族关系
在根树中,若从结点
如果在根树中规定了每一层上结点的次序,这样的根树称为有序树。
在根树
- 若每个分支点至多有
- 若每个分支点都恰有
- 若
- 若满
- 任一结点
二元有序树
二元有序树的每个结点
满
定理 在满
10.6 根树的遍历
二元树的遍历
二元树的先根次序遍历算法
- 访问根;
- 按先根次序遍历根的左子树;
- 按先根次序遍历根的右子树。
二元树的中根次序遍历算法
- 按先根次序遍历根的左子树;
- 访问根;
- 按先根次序遍历根的右子树。
二元树的后根次序遍历算法
- 按先根次序遍历根的左子树;
- 按先根次序遍历根的右子树;
- 访问根。
表达式的记法
可以用二叉树表示一些复杂的表达式,如复合命题,集合的组合,以及算术表达式。
例:有如下二叉树表示表达式
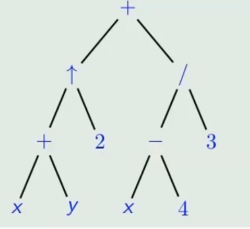
中缀形式:
对表达式的二叉树进行中根遍历时,就得到了它的中缀形式。需要加括号规定运算顺序以防止二义性。
前缀形式:
对表达式的二叉树进行先根遍历时,就得到了它的前缀形式。前缀形式的最大优点是无二义性,所以不再需要括号。
写成前缀形式的表达式称为波兰符号法。表达式的求值方式是从右向左。
后缀形式:
对表达式的二叉树进行后根遍历时,就得到了它的后缀形式。后缀形式同样无二义性,所以也不再需要括号。
写成后缀形式的表达式称为逆波兰符号法。表达式的求值方式是从左向右。
根树的遍历
根树的先根次序遍历算法
- 访问根;
- 按先根次序从左向右遍历根的各子树。
根树的后根次序遍历算法
- 按先根次序从左向右遍历根的各子树;
- 访问根。
10.7 最优树与哈夫曼算法〔扩展内容〕
前缀码
设
设
用二元树产生二元前缀码
给定一棵二元树
最优树
设有一棵二元树
哈夫曼算法
- 初始:令
- 从
- 令
- 判断
第十一章 特殊图
11.1 欧拉图
哥尼斯堡七桥问题
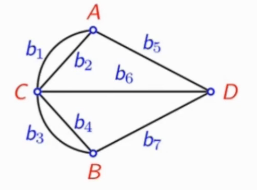
定义
设
规定 平凡图为欧拉图。
欧拉通路是经过图中所有边的通路中长度最短的通路。
欧拉回路是经过图中所有边的回路中长度最短的回路。
判定
无向图
无向图
有向图
有向图
一笔画
所谓一笔画是指笔不离纸、不重复地画出图形。能否一笔画本质上就是求图中是否存在欧拉通路(或欧拉回路)的问题。
求无向图的欧拉回路——Fleury算法
依次选边,每选一条边就从图中删去。选取条件是:
- 与上一条已选取的边关联;
- 除非无别的边可选,否则不能选割边(桥)。
中国邮路问题
一个邮递员送信,要走完他负责投递的全部街道,完成任务后回到邮局。那么,应该按怎样的路线走,他所走的路程才会最短?
解 首先转化为图论问题:在一个无向赋权连通图中求一条回路,使其总权值最小。
如果此无向图为欧拉图,则使用Fleury算法直接求欧拉回路即可。
否则,有些边必须重复经过,相当于在原图中添加了一些平行边。从而,只要保证这些平行边的权值最小就行了。
定义 (中国邮路问题)在一个有奇度数结点的赋权连通图中,增加一些平行边,使得新图不含奇度数结点,并且增加的边的总权值最小。
算法
设
- 使用Floyd算法计算图中任意两点间的最短通路长度;
- 构成一个
- 将矩阵中的结点进行两两组合,找出一个最佳的组合情况,这种组合使得它们的最短通路长度之和最小;
- 根据这个最佳组合,求出各对组合的最短通路,并将最短通路上的每条边都加一条平行边。
11.2 哈密顿图
周游世界问题
要求沿正十二面体的边寻找一条路通过20个城市,而每个城市只通过一次,最后返回原地。
定义
设
规定 平凡图为哈密顿图。
哈密顿通路是经过图中所有结点的通路中长度最短的通路。
哈密顿回路是经过图中所有结点的回路中长度最短的回路。
必要条件
定理 设无向图
推论 设无向图
此定理是哈密顿图的必要条件,而不是充分条件。
此定理的主要应用是判断某些图不是哈密顿图,即:若存在
有割点的图一定不是哈密顿图。
充分条件
定理 设
定理 设
推论 设
定理及其推论给出的是哈密顿图的充分条件,而不是必要条件。
TSP问题
巡回售货员问题也称为货郎担问题。有一个售货员,从他所在城市出发去访问
个城市,要求经过每个城市恰好一次,然后返回原地。如何安排他的旅行路线才能保证最短?
问题 设
解 找出所有可能的哈密顿回路并计算每条回路的总权值,得到最短通路。
当
11.3 偶图
偶图
若无向图
完全偶图
在偶图
偶图的判定
定理 无向图
根据偶图的充分必要条件,我们可将平凡图和零图看成特殊的偶图。
常用其逆否命题来判断一个图不是偶图:无向图
偶图的匹配
在偶图
匹配实际上就是在偶图
匹配的判定条件
定理 (霍尔定理)偶图
定理 (
则
11.4 平面图
平面图
如果能够把一个无向图
例:平面图
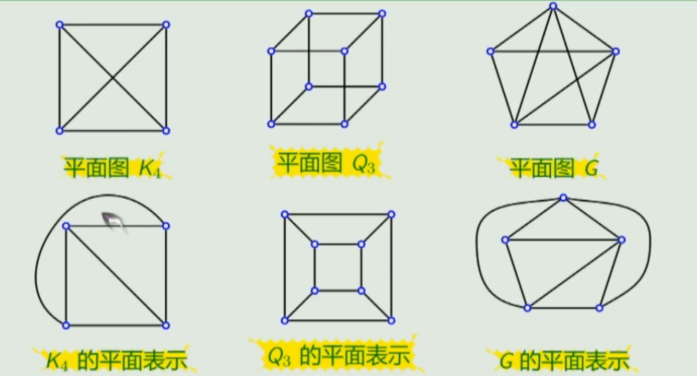
例:非平面图
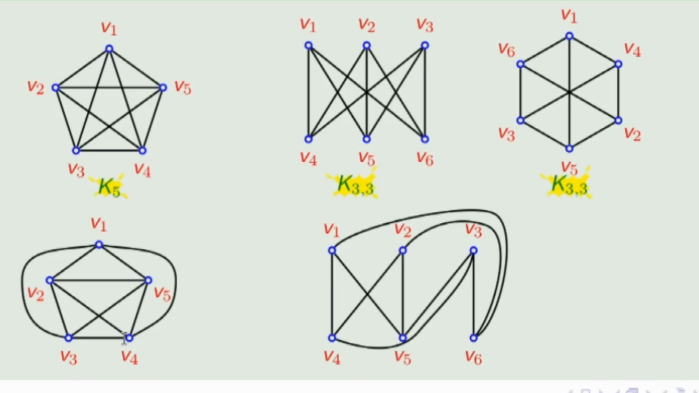
平面图的面
在平面图
例:

面的概念也可以用下面形象的说法加以描述:
假设我们把一个平面图的平面表示画在平面上,然后用一把小刀,沿着图的边切开,那么平面就被切成许多块,每一块就是图的一个面。更确切地说,平面图的一个面就是平面的一块,它用边作边界线,且不能再分成子块。
另外,对于同一平面图的不同平面表示(例如下图中,将
放在里面),虽然面的数目相同,但写出的边界和对应的次数可以不同。 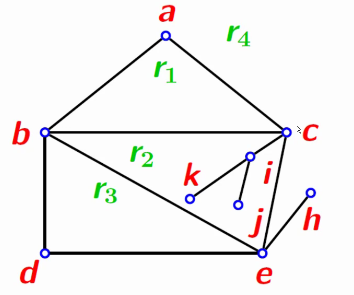
定理 平面图的所有面的次数之和等于边数的二倍。
欧拉公式
1750年,欧拉发现,任何一个凸多面体,若有
个顶点、 条棱和 个面,则有 .这个公式可以推广到平面图上来(球极投影),称之为欧拉公式。
定理 设
平面图的必要条件
推论 设
该推论是必要条件。即,一个简单连通图,若不满足
,则一定是非平面图。
推论 设
该推论是必要条件。即,一个简单连通图,若每个面的次数至少为
,若不满足 ,则一定是非平面图。
库拉托夫斯基定理
同胚
如果两个图
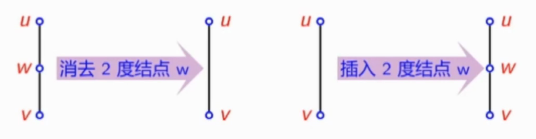
收缩
图中边
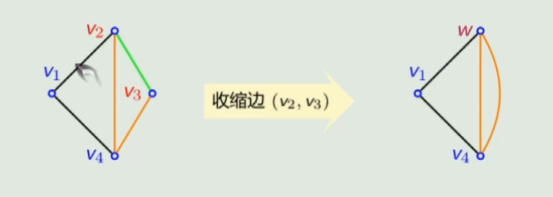
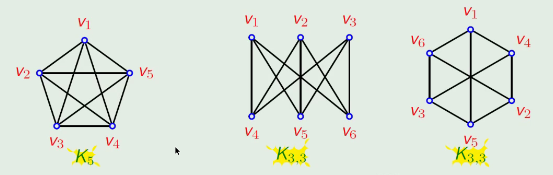
库拉托夫斯基定理
定理 一个图是平面图的充分必要条件是它的任何子图都不与
定理 一个图是平面图的充分必要条件是它的任何子图都不能收缩为
复习要点
以下是笔者所参加课程之考纲要求。各院校专业与教授风格皆大相径庭,读者应审慎参考,不应盲从所述。
凡〔扩展内容〕一概不考。
集合
- 可数集合、不可数集合
- 包含
- 集合的定义
数理逻辑
- 自由变元、约束变元
- 推理规则(US等等)
- 主析取、合取范式(必考)
- 谓词逻辑推理(必考)
- 前置:命题逻辑推理
- 命题符号化
- 演绎法:后面的
- 公式类型:重言式、可满足式、矛盾式等
- 基本等价关系
关系理论
- 二元关系
- 基本运算:复合运算、逆运算
- 性质:自反、传递等;保守性
闭包不考
- 特殊关系(常考)
- 等价
- 次序:拟序、良序、偏序(必考)等
- 函数
置换函数不考
- 概念
- 复合运算
- 性质
图论
- 图
- 最短通路(掌握 Dijkstra 和 Floyd 其一即可)
中国邮递员等两个问题不考
- 树
- 最小生成树(掌握其一即可)
- 特殊图
- 平面图:
对偶、着色不考 - 欧拉图等图的概念
- 偶图、子图、完全图、补图等的概念(能判定)
- 偶图:能判定其匹配
- 平面图:
〔离散数学 完〕
